Суперкомпьютер рассчитал самое большое математическое доказательство, объем данных которого составил 200 терабайт - «Наука и технологии»

Трое ученых, Мэриджн Хеул (Marijn Heule) из Техасского университета, Оливер Куллман (Oliver Kullmann) из университета Суонси и Виктор Марек (Victor Marek) из университета Кентукки загрузили суперкомпьютер задачей поиска доказательства одной из известных математических проблем. Для поиска этого доказательства суперкомпьютеру требовалось "перемолотить" более триллиона цветовых комбинаций и в результате расчетов суперкомпьютер произвел на белый свет самое объемное математическое доказательство на сегодняшний день, объем данных которого составляет 200 терабайт.

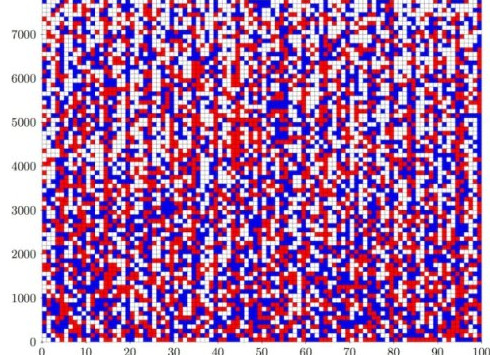
Решаемая суперкомпьютером проблема называется проблемой булевых пифагоровых троек (Boolean Pythagorean Triples Problem), автором этой проблемы, которая появилась на свет в 1980-х годах, является ученый-математик Рональд Грэм из Калифорнийского университета в Сан-Диего. Суть проблемы заключается в поиске в ряде натуральных чисел троек чисел a, b и с, удовлетворяющих теореме Пифагора a^2 + b^2 = c^2. При этом, если условно окрасить числа в цвета, синий и красный, к примеру, то все числа пифагоровой тройки не должны быть окрашены в один цвет. В качестве примера рассмотрим пифагорову тройку 3, 4 и 5, если 3 и 5 окрашены в синий цвет, то 4 должна быть окрашена в красный. При этом, весь процесс разделения чисел на цвета должен быть проведен при помощи булевских (логических) переменных.

Неискушенному в математике человеку такая задача может показаться абсолютной бессмыслицей. Тем не менее, эта проблема имеет прямое отношение к теории Рамсея, к области математики, в которой изучаются критерии, при которых в случайно сформированных массивах или других математических объектах появляется некоторая упорядоченность. Все задачи в теории Рамсея сводятся к поискам ответа на вопрос: "сколько случайных чисел или элементов должен содержать объект, чтобы он гарантировано обрел упорядоченную структуру".